Как найти координаты точки пересечения графиков функций?

Методики нахождения точек

Чтобы узнать, пересекаются ли графики функций, нужно приравнять соответствующие тождества, а затем решать уравнение. Однако при такой операции могут получиться различные равенства с неизвестными

В этом случае требуется обратить внимание на нижеописанные методики решения для каждого вида

Первой и второй степени

Уравнение первой степени, или линейное, решается очень просто. Для этого необходимо перенести переменные величины в одну, а известные — в другую сторону. Методика решения имеет следующий вид:

1. Раскрыть скобки и привести подобные коэффициенты.
2. Выполнить перенос известных в одну, а неизвестных — в другую часть равенства.
3. Произвести необходимые математические преобразования.
4. Найти корень.

Сложнее решается квадратное уравнение. Существует несколько способов нахождения его корней:

1. Разложить на множители.
2. Выделить полный квадрат.
3. Найти дискриминант.
4. По теореме Виета.

Первый способ применяется довольно часто, поскольку с его помощью можно понижать степень при неизвестной величине. Второй подразумевает выделение квадрата по одной из формул сокращенного умножения. Чтобы воспользоваться одним из двух методов, необходимо знать соответствующие тождества (правила разложения на множители).

Однако не всегда можно быстро решить квадратное уравнение при помощи первых двух методов. Еще один вариант — нахождение корней через дискриминант (Д), т. е. дополнительный параметр, позволяющий сразу находить решения. Он находится по следующей формуле: Д=(-S)^2 -4PU.

Следует отметить, что при Д>0 переменная принимает два значения, которые превращают равенство в истину. Если Д=0, то корень только один. Когда Д<0, искомое тождество с неизвестными вообще не имеет решений. Определить значение корней возможно по таким соотношениям: t1=[-S-(Д)^(1/2)]/2P и t2=[-S+(Д)^(1/2)]/2P, где t1 и t2 — точки пересечения с осью абсцисс.

Если коэффициент при второй степени (P) эквивалентен 1, то дискриминант можно не высчитывать, а воспользоваться сокращенным вариантом решения — теоремой Виета. Суть ее заключается в подборе корней по таким формулам: t1+t2=-S и t1*t2=U. Иногда для реализации этой методики нужно сократить обе части на коэффициент Р. Алгоритм решения квадратных уравнений имеет следующий вид:

1. Выполнить при необходимости различные алгебраические преобразования (раскрыть скобки и привести подобные слагаемые).
2. Выбрать один из способов решения и реализовать его.
3. Проверить корни, подставив их в исходное выражение.

Следует отметить, что распространенная ошибка новичков — отсутствие проверки. В результате неправильных действий образуются ложные корни, а оценка на контрольной, зачете или экзамене существенно снижается.

Кубические и биквадратные

Решение тождеств кубического и биквадратного типов с неизвестными осуществляется двумя способами. К ним относятся:

1. Понижение степени (разложение на множители).
2. Замена переменной.

В первом случае необходимо выполнить преобразования, которые позволят применить одну из формул сокращенного умножения. Однако этот метод применяется довольно редко, поскольку математики отдают предпочтение второму способу. Для его реализации вводится дополнительная переменная, обладающая более низкой степенью и существенно упрощающая выражение. Алгоритм имеет такой вид:

1. Выполняются необходимые математические преобразования.
2. Выражается переменная через другую.
3. Решается квадратное или линейное уравнение.
4. Промежуточные корни, полученные в третьем пункте алгоритма, подставляются во второй.
5. Вычисляются искомые корни.
6. Осуществляется проверка.
7. Отсеиваются ложные решения, и записывается ответ.

Для проверки рекомендуется воспользоваться онлайн-приложениями, позволяющими вычислить корни, а также построить графики функций. Кроме того, для кубического многочлена Pt 3 +St 2 +Ut+V=0 существует еще одна методика нахождения корней. Она имеет следующий вид:

1. Уравнение требуется разделить на P.
2. Осуществить замену: t=m-(S/(3P)). При этом получается тождество вида m^3 +km+l=0.
3. Найти значение коэффициентов по формулам: k= / (27P 3 ) и l=[(3PU-S 2 )/(3P 2 )]. Подставить их во второй пункт и найти промежуточные корни, при помощи которых найти основные значения переменных.

Следует отметить, что важным пунктом методики является правильный выбор выражения замены, а затем верное выполнение математических преобразований.

Практика 2

В дополнение к функции нахождения точки пересечения, напишем «продвинутую» функцию, которая находит эту точку, определяет нахождение на каждом из отрезков, и определяет угол между направляющими векторами. Или же определяет, что прямые параллельны/совпадают.

//**********************************************************
// Тип пересечения прямых (p1,p2) и (p3,p4)
//**********************************************************
type
TxCrossLineResult = (
xclrEqual = -32// эквивалентны
,xclrParallel = -16// параллельны
,xclrOk = 0 // как минимум пересечение есть
,xclrFirst = 1 // попадает в первый отрезок
,xclrSecond = 2 // попадает во второй отрезок
,xclrBoth = 3 // попадает в оба
,xclrPerpend = 4 // перпендикулярны
// можно найти по маске через AND, но для полноты картины
,xclrFirstP = 5 // перпендикулярны и попадает в первый
,xclrSecondP = 6 // перпендикулярны и попадает в второй
,xclrBothP = 7 // перпендикулярны и попадает в оба
);

//**********************************************************
// Нахождение точки пересечения прямых (p1,p2) и (p3,p4)
// Определяет параллельность, совпадение,
// перпендикулярность, пересечение.
// Определяет, каким отрезкам принадлежит.
// Находит угол(рад.) от (p1,p2) к (p3,p4):
// отрицательное значение — против часовой
// положительное — по часовой
//**********************************************************
function CrossLines(const p1,p2,p3,p4: TxPoint;
var res: TxPoint; var Angle: Extended): TxCrossLineResult;
const
Prec = 0.0001;
var
a1, a2: Extended;
b1, b2: Extended;
c1, c2: Extended;
v: Extended;
begin
Angle := 0;

a1 := p2.y — p1.y;
a2 := p4.y — p3.y;

b1 := p1.x — p2.x;
b2 := p3.x — p4.x;

c1 := p2.x*p1.y — p1.x*p2.y;
c2 := p4.x*p3.y — p3.x*p4.y;

v := a1*b2 — a2*b1;

if abs(v) > Prec then
begin
Result := xclrOk;

res.X := -(c1*b2 — c2*b1)/v;
res.Y := -(a1*c2 — a2*c1)/v;

if CheckCrossPoint(p1,p2,res) then
Result := TxCrossLineResult(Integer(Result) +
Integer(xclrFirst));

if CheckCrossPoint(p3,p4,res) then
Result := TxCrossLineResult(Integer(Result) +
Integer(xclrSecond));

if (abs(a1*a2 + b1*b2) < Prec) then
Result := TxCrossLineResult(Integer(Result) +
Integer(xclrPerpend));

Angle := CalcCrossAngle(a1,b1,a2,b2);
end else
begin
Result := xclrParallel;
if ((abs(c1*b2 — c2*b1) < Prec) and
(abs(a1*c2 — a2*c1) < Prec))
then
Result := xclrEqual;
end;
end;

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80

//********************************************************** //  Тип пересечения прямых (p1,p2) и (p3,p4) //********************************************************** type TxCrossLineResult=( xclrEqual=-32// эквивалентны ,xclrParallel=-16// параллельны ,xclrOk=// как минимум пересечение есть ,xclrFirst=1// попадает в первый отрезок ,xclrSecond=2// попадает во второй отрезок ,xclrBoth=3// попадает в оба ,xclrPerpend=4// перпендикулярны // можно найти по маске через AND, но для полноты картины ,xclrFirstP=5// перпендикулярны и попадает в первый ,xclrSecondP=6// перпендикулярны и попадает в второй ,xclrBothP=7// перпендикулярны и попадает в оба );   //********************************************************** //  Нахождение точки пересечения прямых (p1,p2) и (p3,p4) //  Определяет параллельность, совпадение, //  перпендикулярность, пересечение. //  Определяет, каким отрезкам принадлежит. //  Находит угол(рад.) от (p1,p2) к (p3,p4): //    отрицательное значение — против часовой //    положительное — по часовой //********************************************************** functionCrossLines(constp1,p2,p3,p4TxPoint; varresTxPoint;varAngleExtended)TxCrossLineResult; const Prec=0.0001; var a1,a2Extended; b1,b2Extended; c1,c2Extended; vExtended; begin Angle=; a1=p2.y-p1.y; a2=p4.y-p3.y; b1=p1.x-p2.x; b2=p3.x-p4.x; c1=p2.x*p1.y-p1.x*p2.y; c2=p4.x*p3.y-p3.x*p4.y; v=a1*b2-a2*b1; ifabs(v)>Prec then begin Result=xclrOk; res.X=-(c1*b2-c2*b1)/v; res.Y=-(a1*c2-a2*c1)/v; ifCheckCrossPoint(p1,p2,res)then Result=TxCrossLineResult(Integer(Result)+ Integer(xclrFirst)); ifCheckCrossPoint(p3,p4,res)then Result=TxCrossLineResult(Integer(Result)+ Integer(xclrSecond)); if(abs(a1*a2+b1*b2)<Prec)then Result=TxCrossLineResult(Integer(Result)+ Integer(xclrPerpend)); Angle=CalcCrossAngle(a1,b1,a2,b2); endelse begin Result=xclrParallel; if((abs(c1*b2-c2*b1)<Prec)and (abs(a1*c2-a2*c1)<Prec)) then Result=xclrEqual; end; end;

Как это кодить в C++

Небольшой ликбез по объектно-ориентированному программированию в C++. Создадим класс, который будет отвечать за все операции с точками. В C++ есть два способа это сделать: через и через . Их основное отличие в том, что по умолчанию в все поля приватные — к ним нет прямого доступа снаружи. Это нужно для дополнительной защиты, чтобы в крупных промышленных проектах никто случайно ничего не поломал, но на олимпиадах это не очень актуально.

Точка \(\simeq\) вектор. Будем считать точка и вектор это один и тот же объект, так как они оба — это просто пара чисел. Будем сопоставлять точке её радиус-вектор — вектор из начала координат, ведущий в эту точку. По принятой в математике и физике нотации, будем обозночать вектора как . Вы можете обозвать их как , , — как угодно.

Функция внутри класса вызывается при инциализации объекта. Её называют конструктором, и её можно указывать разную для разных параметров. Здесь вернёт точку с неопределенными (какие оказались в памяти в тот момент) координатами, а вернет точку с координатами \((x, y)\).

Операторы

В C++ можно перегружать почти все стандартные операторы, например, , , и т. д.

Переопределим для будущих нужд и :

Скалярное произведение:

Векторное произведение:

Цепляясь за лед (2020)

В мотивирующем сериале про спортсменов серьезная травма ставит крест на карьере талантливой фигуристки – девушка больше не может выполнять сложные прыжки. Тренер предлагает спортсменке заняться парным катанием. Героине достается проблемный партнер, которому бы больше подошло заниматься хоккеем. У этого хулиганистого парня крутой характер и множество вредных привычек. Через нервные срывы, финансовые трудности, бесконечные конфликты и упорные тренировки пара будет идти к чемпионскому титулу.

Оригинальное названиеSpinning OutЖанрДрамаАктерыКая Скоделарио, Дженьюэри Джонс, Уиллоу Шилдс…СтранаСШАРейтингКинопоиск – 6.9, IMDb – 7.6

Свойства и соотношения

На основании теоремы о биссектрисах Δ были получены некоторые важные свойства, которые рекомендуется применять при решении задач и доказательства других утверждений:

1. Центр вписанной окружности соответствует точке их пересечения.
2. Точка при пересечении делит биссектрису по такому соотношению: отношение суммарного значения прилежащих к противолежащей стороне.
3. Угол между биссектрисами двух смежных углов является прямым.
4. В равнобедренном Δ равны только 2 биссектрисы, а в равностороннем — 3. Кроме того, она является медианой и высотой.

При решении задач нужно находить их длину (L).

Для удобства необходимо обозначить стороны таким образом: КМ = d, КL = e и LМ = f, чтобы воспользоваться следующими формулами через известные параметры треугольника:

1. Все стороны: Lm = / (d + e), Lк = / (d + f) и Ll = / (d + f). Параметр «р» — полупериметр, т. е. р = (d + e + f) / 2.
2. Стороны и угол: Lm = (2 * d * e * cos (∠M)) / (d + e), Lk = (2 * d * f * cos (∠K)) / (d + f) и Ll = (2 * f * e * cos (∠L)) / (f + e).

Соотношения позволяют найти не только длины Lk, Lm и Ll, но и другие параметры треугольников. Следует отметить, что углы во второй группе формул соответствуют биссектрисам, исходящим из них.

Таким образом, для решения задач на нахождение длины биссектрис необходимо знать теорию, доказательство теоремы, свойства, а также основные соотношения.

2 ответа

Стандартный способ решения таких задач – использовать параметрическую запись прямой, заданной направляющим вектором и точкой: $$eginx=mt+x_0,\y=nt+y_0,\z=pt+z_0.end$$ Здесь $%(m,n,p)$% – координаты вектора от одной точки до другой, а $%(x_0,y_0,z_0)$% – координаты одной из точек. Подставляете эти значения в уравнение плоскости, откуда находите параметр $%t$%. По этому параметру находите $%(x,y,z)$%.

Задача

Даны два отрезка, каждый из которых задан двумя точками: (v11, v12), (v21, v22). Необходимо определить, пересекаются ли они, и если пересекаются, найти точку их пересечения.

Решение

Для начала необходимо определить, пересекаются ли отрезки. Необходимое и достаточное условие пересечения, которое должно быть соблюдено для обоих отрезков следующее: конечные точки одного из отрезков должны лежать в разных полуплоскостях, если разделить плоскость линией, на которой лежит второй из отрезков. Продемонстрируем это рисунком. На левом рисунке (1) показаны два отрезка, для обоих из которых условие соблюдено, и отрезки пересекаются. На правом (2) рисунке условие соблюдено для отрезка b, но для отрезка a оно не соблюдается, соответственно отрезки не пересекаются. Может показаться, что определить, с какой стороны от линии лежит точка — нетривиальная задача, но у страха глаза велики, и всё не так сложно. Мы знаем, что векторное умножение двух векторов даёт нам третий вектор, направление которого зависит от того, положительный или отрицательный угол между первым и вторым вектором, соответственно такая операция антикоммутативна. А так как все вектора лежат на плоскости X-Y, то их векторное произведение (которое обязано быть перпендикулярным перемножаемым векторам) будет иметь ненулевой только компоненту Z, соответственно и отличие произведений векторов будет только в этой компоненте. Причем при изменении порядка перемножения векторов (читай: угла между перемножаемыми векторами) состоять оно будет исключительно в изменении знака этой компоненты. Поэтому мы можем умножить попарно-векторно вектор разделяющего отрезка на векторы направленные от начала разделяющего отрезка к обеим точкам проверяемого отрезка. Если компоненты Z обоих произведений будет иметь различный знак, значит один из углов меньше 0 но больше -180, а второй больше 0 и меньше 180, соответственно точки лежат по разные стороны от прямой. Если компоненты Z обоих произведений имеют одинаковый знак, следовательно и лежат они по одну сторону от прямой. Если один из компонент Z является нулём, значит мы имеем пограничный случай, когда точка лежит аккурат на проверяемой прямой. Оставим пользователю определять, хочет ли он считать это пересечением. Затем нам необходимо повторить операцию для другого отрезка и прямой, и убедиться в том, что расположение его конечных точек также удовлетворяет условию. Итак, если всё хорошо и оба отрезка удовлетворяют условию, значит пересечение существует. Давайте найдём его, и в этом нам также поможет векторное произведение. Так как в векторном произведении мы имеем ненулевой лишь компоненту Z, то его модуль (длина вектора) будет численно равен именно этой компоненте. Давайте посмотрим, как найти точку пересечения. Длина векторного произведения векторов a и b (как мы выяснили, численно равная его компоненте Z) равна произведению модулей этих векторов на синус угла между ними (|a| |b| sin(ab)). Соответственно, для конфигурации на рисунке мы имеем следующее: |AB x AC| = |AB||AC|sin(α), и |AB x AD| = |AB||AD| sin(β). |AC|sin(α) является перпендикуляром, опущенным из точки C на отрезок AB, а |AD|sin(β) является перпендикуляром, опущенным из точки D на отрезок AB (катетом ADD’). Так как углы γ и δ — вертикальные углы, то они равны, а значит треугольники PCC’ и PDD’ подобны, а соответственно и длины всех их сторон пропорциональны в равном отношении. Имея Z1 (AB x AC, а значит |AB||AC|sin(α) ) и Z2 (AB x AD, а значит |AB||AD|sin(β) ), мы можем рассчитать CC’/DD’ (которая будет равна Z1/Z2), а также зная что CC’/DD’ = CP/DP легко можно высчитать местоположение точки P. Лично я делаю это следующим образом:

Px = Cx + (Dx-Cx)*|Z1|/|Z2-Z1|; Py = Cy + (Dy-Cy)*|Z1|/|Z2-Z1|;

Вот и все. Мне кажется что это действительно очень просто, и элегантно. В заключение хочу привести код функции, реализующий данный алгоритм. В функции использован самодельный шаблон vector , который является шаблоном вектора размерностью int с компонентами типа typename. Желающие легко могут подогнать функцию к своим типам векторов.

Если точка M, является точкой пересечения двух прямых, то она должна принадлежать этим прямым, а ее координаты удовлетворять уравнения этих прямых.

Секреты и пасхалки

Марк Трасс

Отсылка к Дональду Трампу.

В игре есть плакат с неким Марком Трассом, а внизу лозунг – «Давайте сделаем область залива сильнее!».

Что случилось с Эйденом Пирсом из оригинальной Watch Dogs

В одной из миссий игры, если взломать камеру, можно увидеть Эйдена Пирса, являющегося главным героем предыдущей игры. Пирс сидит в клетке, но мы можем ему помочь, вследствие чего он сможет устранить охранника и сбежать.

Офис Ubisoft

Вы можете найти офис компании Ubisoft, которая и создала Watch Dogs 2. Стоит отметить, что разработчики также сделали подобную пасхалку в The Division. Примечательно, что рядом с надписью Ubisoft можно увидеть огромный постер фильма «Кредо Убийцы». На крыше, кстати, находится цифровая его версия.

Трейлер таинственной игры про космос

Если вы все же проберетесь внутрь офиса Ubisoft и взломаете доступ ко всей файлам, то сможете просмотреть трейлер какой-то таинственной игры, чем-то напоминающей No Man’s Sky. Возможно, таким вот способом игроделы тизерят свою будущую игру, действие которой развернется в космосе.

Gary’s Games & Glory — Games Workshop

Посетите небольшой магазинчик, который пропитан культурой американских ботаников и настольными играми. В магазине даже есть что-то напоминающее настольную игру Magic: The Gathering.

Внедорожник из фильма Парк Юрского периода

Игра включает в себя огромнейшее количество уникальных машин. Одной из таких является внедорожник из фильма «Парк Юрского периода». Он находится далеко на востоке карты. Вы сразу сможете заметить его благодаря соответствующей расцветке. Попробуйте включить сигнал, и услышите дикое рычание динозавра, а экран при этом будет трясти.

Отсылка к Rainbow Six: Siege

В начале игры, когда вы будете изучать свои хакерские способности, то сможете увидеть, как некий Крис Пинкл играет в тактический шутер от первого лица Rainbow Six: Siege. К сожалению, вы не сможете взломать игру, но понаблюдать за происходящим довольно интересно.

Заведение Papa John’s из The Division

В игре есть заведение Papa Bless/Papa John’s, которое также присутствует и в The Division. Рассмотрите его целостный вид, ведь в The Division оно находится не в самом лучшем состоянии.

Много голых людей

В первых версиях Watch Dogs 2 есть люди, которые полностью обнаженные. Ubisoft добавила к частям тел персонажей даже гениталии, что вызвало много шумихи, когда геймеры начали делиться скриншотами и видеороликами с подобными персонажами.

Костюм гнома

По всему внутриигровому Сан-Франциско разбросано множество статуй гномов. Если вы соберете все их части, то получите костюм гнома, в котором Маркус сможет творить свои деяния. Неплохой косплей?!

Намек на Assassin’s Creed: Origins

Если взломать телефонный разговор одного из персонажей, то можно услышать, как кто-то говорит о некой Assassin’s Creed: Osiris. Интересно, является ли это намеком на новую игру в серии?

https://youtube.com/watch?v=QEgIYEfod9U

DedSec – это Анонимус

Есть множество деталей, которые связывают DedSec с хакерской группировкой Анонимус. Некоторые видеоролики, которые выкладывают внутриигровые персонажи из DedSec очень сильно напоминают таковые от Анонимус.

Секретный Коровий Уровень из Diablo 2

Если внимательно слушать все внутриигровые диалоги между персонажами, можно услышать, как один из них говорит, что получил доступ к Секретному Коровьему Уровню. Если вы не знаете, Коровий уровень впервые появился в Diablo 2, и позволял игрокам получать различные бонусы а противоположному вселенной Diablo мире.

Nudle – это Google

В игре есть множество упоминаний о некой Nudle. К примеру вы сможете пользоваться навигатором Nudle Maps, что безусловно относится к Google в реальном мире.

Кибертачка

Вы можете получить настоящую кибермашину с эквалайзером поверх бампера. То как можно получить данную тачку, рассказано в видеоролике ниже:

Что это, Assassin’s Creed Orgy-ins?

И, наконец, конечно, Древний Египет имеет зрелое отношение к сексу в этом наиболее цивилизованном мире. Прогуляйтесь мимо борделя в Ираклионе в Ираклионе номе, и вы услышите несколько очень характерных шумов, исходящих из комнаты наверху. Поднимитесь, как заинтересованный ассасин, и если вы загляните в это окно, как обычный «Подглядывающий Том», вы можете получить визуальные эффекты, которые подойдут к вашему аудио. Подобно преследователю папарацци, функция масштабирования вашего фоторежима очень пригодится, чтобы увидеть явные рисунки на стенах и очень занятых людей на полу. Я уверен, что это не то, о чем думала Ubi, когда добавила невероятный режим фото. Да. Наслаждайтесь ощущением не того слова …

Да, в Assassin’s Creed Origins есть оргии. Вот как это найти

Нахождение координат точки пересечения двух прямых в пространстве.

Координаты точки пересечения двух прямых в трехмерном пространстве находятся аналогично.

Пусть пересекающиеся прямые a и b заданы в прямоугольной системе координат Oxyzуравнениями двух пересекающихся плоскостей, то есть,  a определяется системой вида , а прямая b — . Пусть М – точка пересечения прямых a и b. Тогда точка М по определению принадлежит и прямой a и прямойb, следовательно, ее координаты удовлетворяют уравнениям обеих прямых. Таким образом, координаты точки пересечения прямых a и b представляют собой решение системы линейных уравнений вида . Здесь нам пригодится информация из разделарешение систем линейных уравнений, в которых число уравнений не совпадает с числом неизвестных переменных.

Рассмотрим решения примеров.

Пример.

Найдите координаты точки пересечения двух прямых, заданных в пространстве уравнениями  и .

Решение.

Составим систему уравнений из уравнений заданных прямых: . Решение этой системы даст нам искомые координаты точки пересечения прямых в пространстве. Найдем решение записанной системы уравнений.

Основная системы имеет вид , а расширенная — .

Определим ранг матрицы А и ранг матрицы T. Используем метод окаймляющих миноров, при этом не будем подробно описывать вычисление определителей (при необходимости обращайтесь к статье вычисление определителя матрицы):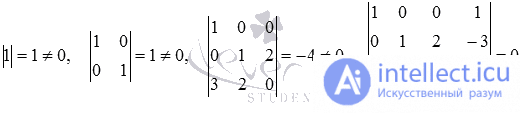

Таким образом, ранг основной матрицы равен рангу расширенной матрицы и равен трем.

Следовательно, система уравнений  имеет единственное решение.

Базисным минором примем определитель , поэтому из системы уравнений следует исключить последнее уравнение, так как оно не участвует в образовании базисного минора. Итак,

Решение полученной системы легко находится: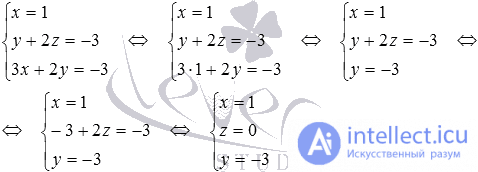

Таким образом, точка пересечения прямых  и  имеет координаты (1, -3, 0).

Ответ:

(1, -3, 0).

Следует отметить, что система уравнений  имеет единственное решение тогда и только тогда, когда прямые a и b пересекаются. Если же прямые а и bпараллельные или скрещивающиеся, то последняя система уравнений решений не имеет, так как в этом случае прямые не имеют общих точек. Если прямые a и b совпадают, то они имеют бесконечное множество общих точек, следовательно, указанная система уравнений имеет бесконечное множество решений. Однако в этих случаях мы не можем говорить о нахождении координат точки пересечения прямых, так как прямые не являются пересекающимися.

Таким образом, если мы заранее не знаем, пересекаются заданные прямые a и b или нет, то разумно составить систему уравнений вида  и решить ее методом Гаусса. Если получим единственное решение, то оно будет соответствовать координатам точки пересечения прямых a и b. Если система окажется несовместной, то прямые a и b не пересекаются. Если же система будет иметь бесконечное множество решений, то прямые a и bсовпадают.

Можно обойтись и без использования метода Гаусса. Как вариант, можно вычислить ранги основной и расширенной матриц этой системы, и на основании полученных данных и теоремы Кронекера-Капелли сделать вывод или о существовании единственного решения, или о существовании множества решений, или об отсутствии решений. Это дело вкуса.

Пример.

Если прямые  и  пересекаются, то определите координаты точки пересечения.

Решение.

Составим систему из заданных уравнений: . Решим ее методом Гаусса в матричной форме:

Стало видно, что система уравнений не имеет решений, следовательно, заданные прямые не пересекаются, и не может быть и речи о поиске координат точки пересечения этих прямых.

Ответ:

мы не можем найти координаты точки пересечения заданных прямых, так как эти прямые не пересекаются.

Когда пересекающиеся прямые заданы каноническими уравнениями прямой в пространствеили параметрическими уравнениями прямой в пространстве, то следует сначала получить их уравнения в виде двух пересекающихся плоскостей, а уже после этого находить координаты точки пересечения.

Пример.

Две пересекающиеся прямые заданы в прямоугольной системе координат Oxyzуравнениями  и . Найдите координаты точки пересечения этих прямых.

Решение.

Зададим исходные прямые уравнениями двух пересекающихся плоскостей:

Для нахождения координат точки пересечения прямых осталось решить систему уравнений . Ранг основной матрицы этой системы равен рангу расширенной матрицы и равен трем (рекомендуем проверить этот факт). В качестве базисного минора примем , следовательно, из системы можно исключить последнее уравнение . Решив полученную систему любым методом (например методом Крамера) получаем решение . Таким образом, точка пересечения прямых  и  имеет координаты (-2, 3, -5).

Ответ:

(-2, 3, -5).

Существует очень четкая ссылка на сторожевых собак

Широко известно, что вселенные Assassin’s Creed и Watch Dogs связаны между собой. Мы нашли сотрудников Abstergo в Watch Dogs, и даже в Black Flag есть документ о гнусной корпорации Bloom. Теперь один кусочек пасхального яйца принес полную связь. Возможно, вы помните миссию конвоя с криминалом в оригинальных сторожевых псов под названием Requiscat in Pace. Это видело, что Эйден Пирс собирается убить Оливье Гарно, главного креативного директора Abstergo Entertainment. Войдите на ноутбук Лейлы Хасан в настоящее время в AC Origins, и вы найдете папку о нем и реальных скриншотах Оливье, сбитого кем-то в очень узнаваемой бейсболке и шарфе … Давайте просто не будем думать о том факте, что мы украли файлы из вымышленной версии Ubisoft, которая раскрыла новую настоящую игру в Watch Dogs 2… 

Общие сведения

Треугольник — геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и отрезков, соединяющих их. Точки имеют другое название — вершины. Обозначается треугольник символом Δ, после которого идут 3 латинских буквы. Например, ΔMNO. Допускается использовать и русские литеры, но злоупотреблять этим не стоит.

В высших учебных заведениях преподаватели требуют от студентов международное обозначение. Кроме того, большинство программных продуктов и онлайн-сервисов воспринимают только латинские символы.

Классификация треугольников

Необходимо отметить, что Δ различаются между собой по некоторым критериям.

Они бывают нескольких типов:

1. Произвольные.
2. Прямоугольные.
3. Равнобедренные.
4. Равносторонние.
5. Тупоугольные.
6. Остроугольные.

В первом случае стороны фигуры не равны между собой. Чтобы идентифицировать прямоугольный треугольник, необходимо рассмотреть его углы. Если один из них является прямым (равен 90 градусам), такая фигура называется прямоугольной. В третьем виде основным критерием считается наличие двух, равных между собой сторон.

В равностороннем треугольнике все стороны равны между собой. Математики его называют «правильным». Он обладает важным свойством — вокруг него можно описать окружность. Пятый тип определяет наличие тупого угла, градусная мера которого больше 90. Если фигура является остроугольной, это значит, что все 3 его угла меньше 90, т. е. являются острыми.

Один треугольник может относиться к нескольким типам. Например, прямоугольный Δ может быть равнобедренным на основании свойства геометрии: если Δ является равнобедренным, то углы (∠), образованные боковыми сторонами с основанием, равны между собой. В этом случае их градусные меры эквивалентны 45, поскольку сумма ∠ любого Δ составляет 180. Следовательно, 180 — 90 = 2k, где неизвестная величина «к» соответствует углу при основании.

Дополнительные элементы

У любого Δ существуют определенные дополнительные элементы, необходимые при построении чертежей или схематических рисунков, доказательства теорем и решения задач по геометрии.

К ним относятся:

1. Биссектриса.
2. Медиана.
3. Высота.

Биссектриса — отрезок (прямая), проходящий через вершину Δ и делящий угол на 2 равные части. Медиана — единственный отрезок для каждой вершины, соединяющий ее с серединой стороны, на которую он опущен.

Высотой является перпендикуляр, опущенный из вершины на противоположную сторону.

В равнобедренном и равностороннем треугольниках биссектриса является медианой и высотой. В последнем случае их можно провести всего 3.